Kam naudojami epicikliniai krumpliaračiai?

Epiciklinės pavarosdar žinomos kaip planetinės pavarų sistemos, dėl savo kompaktiško dizaino, didelio efektyvumo ir universalumo plačiai naudojamos įvairiose pramonės šakose

Šios pavaros daugiausia naudojamos tais atvejais, kai erdvė ribota, tačiau didelis sukimo momentas ir greičio kintamumas yra būtini.

1. Automobilių transmisijos: Epiciklinės pavaros yra pagrindinis automatinių transmisijų komponentas, užtikrinantis sklandų pavarų perjungimą, didelį sukimo momentą esant mažam greičiui ir efektyvų galios perdavimą.
2. Pramoninės mašinos: Jos naudojamos sunkiosiose mašinose dėl gebėjimo valdyti didelius krovinius, tolygiai paskirstyti sukimo momentą ir efektyviai veikti kompaktiškose erdvėse.
3. Aviacija ir kosmosas: Šie krumpliaračiai atlieka labai svarbų vaidmenį orlaivių varikliuose ir sraigtasparnių rotoriuose, užtikrindami patikimumą ir tikslų judesio valdymą sudėtingomis sąlygomis.
4. Robotika ir automatizavimas: Robotikoje epiciklinės pavaros naudojamos siekiant tikslaus judesio valdymo, kompaktiškos konstrukcijos ir didelio sukimo momento ribotose erdvėse.

Kokie yra keturi epiciklinio krumpliaračio rinkinio elementai?

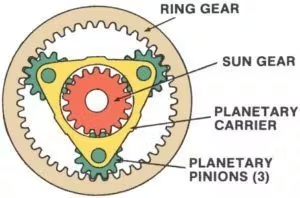
Epiciklinis krumpliaratis, dar žinomas kaipplanetinė pavara sistema yra labai efektyvus ir kompaktiškas mechanizmas, dažniausiai naudojamas automobilių transmisijose, robotikoje ir pramoninėse mašinose. Šią sistemą sudaro keturi pagrindiniai elementai:

1. Saulės pavaraSaulės krumpliaratis, esantis krumpliaračių rinkinio centre, yra pagrindinis judesio variklis arba imtuvas. Jis tiesiogiai jungiasi su planetiniais krumpliaračiais ir dažnai tarnauja kaip sistemos įvestis arba išvestis.

2. Planetinės pavarosTai keli krumpliaračiai, kurie sukasi aplink saulės krumpliaratį. Sumontuoti ant planetarinio laikiklio, jie jungiasi tiek su saulės krumpliaračiu, tiek su žiediniu krumpliaračiu. Planetiniai krumpliaračiai tolygiai paskirsto apkrovą, todėl sistema gali valdyti didelį sukimo momentą.

3.Planetų nešėjasŠis komponentas laiko planetinius krumpliaračius vietoje ir palaiko jų sukimąsi aplink saulės krumpliaratį. Planetos nešiklis gali veikti kaip įvesties, išvesties arba stacionarus elementas, priklausomai nuo sistemos konfigūracijos.

4.Žiedinė pavaraTai didelis išorinis krumpliaratis, kuris juosia planetinius krumpliaračius. Žiedinio krumpliaračio vidiniai dantys susijungia su planetiniais krumpliaračiais. Kaip ir kiti elementai, žiedinis krumpliaratis gali būti įėjimo, išėjimo arba likti nejudanti.

Šių keturių elementų sąveika suteikia lankstumo pasiekti skirtingus greičio santykius ir krypties pokyčius kompaktiškoje konstrukcijoje.

Kaip apskaičiuoti pavaros santykį epicikliniame pavarų komplekte?

Pavarų perdavimo skaičiusepiciklinis krumpliaratis priklauso nuo to, kurie komponentai yra fiksuoti – įvesties ir išvesties. Štai nuoseklus pavaros perdavimo skaičiaus apskaičiavimo vadovas:

1. Supraskite sistemos konfigūraciją:

Nustatykite, kuris elementas (saulė, planeta nešėja ar žiedas) yra nejudantis.

Nustatykite įvesties ir išvesties komponentus.

2. Naudokite pagrindinę pavaros perdavimo skaičiaus lygtį: Epiciklinės pavarų sistemos pavaros perdavimo skaičių galima apskaičiuoti pagal:

GR = 1 + (R / S)

Kur:

GR = Pavarų santykis

R = Žiedinio krumpliaračio dantų skaičius

S = Saulės krumpliaračio dantų skaičius

Ši lygtis taikoma, kai išėjimo šaltinis yra planetų nešėjas, o saulė arba žiedinis krumpliaratis nejuda.

3. Pritaikykite kitoms konfigūracijoms:

• Jei saulės krumpliaratis nejuda, sistemos išėjimo greitį įtakoja žiedinės krumpliaračio ir planetinės laikiklio santykis.
• Jei žiedinė pavara nejuda, išėjimo greitis nustatomas pagal saulės krumpliaračio ir planetinės laikiklio santykį.

4. Atbulinės eigos pavaros santykis išėjimui ir įėjimui: skaičiuojant greičio sumažėjimą (įėjimas didesnis nei išėjimas), santykis yra paprastas. Greičio daugybai (išėjimas didesnis nei įėjimas) apverskite apskaičiuotą santykį.

Skaičiavimo pavyzdys:

Tarkime, kad pavarų komplektas turi:

Žiedinis krumpliaratis (R): 72 dantys

Saulės pavara (S): 24 dantys

Jei planetos nešėjas yra išėjimo šaltinis, o saulės krumpliaratis nejuda, perdavimo skaičius yra:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Tai reiškia, kad išvesties greitis bus 4 kartus mažesnis nei įvesties greitis, todėl redukcijos santykis bus 4:1.

Šių principų supratimas leidžia inžinieriams suprojektuoti efektyvias ir universalias sistemas, pritaikytas konkrečioms reikmėms.